5 khuôn mẫu mạnh mẽ một cách kỳ diệu mà bạn sẽ không tin rằng chúng có mặt ở khắp mọi nơi
Đăng 8 năm trướcGiống như các nghệ sĩ, đôi khi mẹ thiên nhiên thì quá lười biếng để tạo ra các khuôn mẫu mới. Và một vài khuôn mẫu cũ được tái sử dụng trong những tình huống mà bạn sẽ không ngờ tới.
1. Tia sét, nhánh cây, dòng sông và phổi của bạn đều tuân theo cùng một khuôn mẫu


Phía trên là hình dạng vết sét đánh lên thân cây.
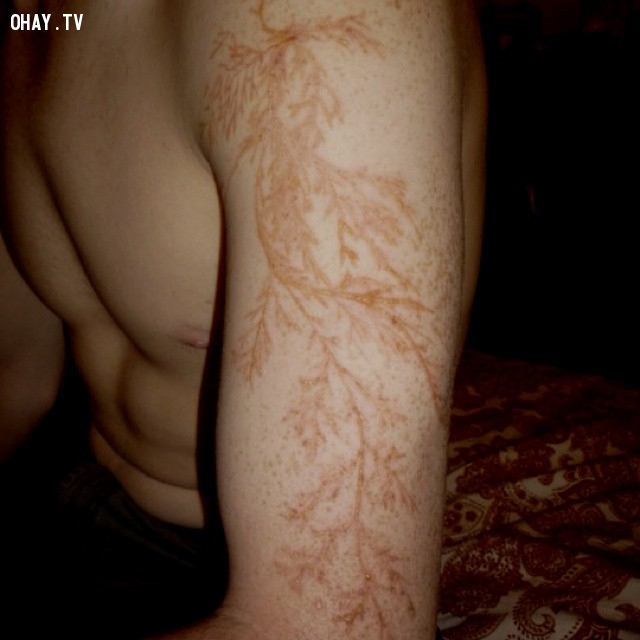
Còn đây là hình ảnh "hoa sét" xuất hiện trên da một nạn nhân bị sét đánh trúng.

Hình ảnh rừng cây trụi lá vào mùa đông.

Hình ảnh những nhánh sông được chụp ở New Zealand
Nếu những hình ảnh trên đều quá vĩ mô, vậy thì hãy xem cấu trúc lá phổi của bạn ở bên dưới.
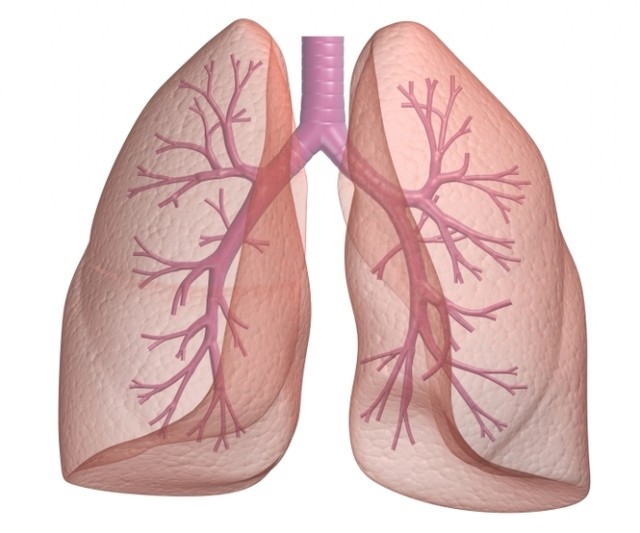
Phổi của người hút thuốc lá trông giống như dãy Fibonacci. Đùa thôi!
Tất cả các đối tượng mà chúng ta vừa xem ở trên đều giống nhau ở một điểm: chúng đều có cấu hình đuôi gai.
Mỗi hệ thống đều có một luồng của cái gì đó, có thể là nước, máu, điện... có xu hướng phân nhánh và chia thành 2 đường.
Cấu hình đuôi gai là một hiện tượng cực kỳ phổ biến xảy ra ở rất nhiều hệ thống khác nhau, cả sinh vật lẫn những đối tượng vô tri vô giác như tia sét, dòng sông...
Trong nhiều tình huống, sự hình thành của cấu hình đuôi gai là kết quả của sự tăng trưởng. Hệ thống dòng chảy đuôi gai tồn tại ở khắp mọi nơi với mọi quy mô khác nhau, từ thực vật cho đến động vật có vú, từ đặc trưng cấu tạo của phổi và hệ thống mạch máu cho tới quá trình sinh trưởng của khuẩn lạc và san hô đá trong môi trường dinh dưỡng thấp. Các nhà khoa học đã tích cực nghiên cứu về cấu hình đuôi gai không chỉ vì ảnh hưởng to lớn của nó trong thiên nhiên mà còn vì những ứng dụng trong ngành công nghiệp. Ví dụ về ảnh hưởng bất lợi là tăng trưởng đuôi gai làm giảm chất lượng của tấm kim loại trong quy trình mạ điện. Ví dụ về ảnh hưởng có lợi là tăng trưởng đuôi gai được sử dụng để cải thiện hiệu ứng xúc tác nhờ các cấu trúc được xây dựng với một giao diện lớn hơn.
Với những ai muốn tìm hiểu sâu hơn về bản chất cũng như khía cạnh toán học của cấu hình đuôi gai, tôi đề nghị bạn bắt đầu với bài viết "Dendritic design as an archetype for growth patterns in nature: fractal and constructal views" của Antonio F. Miguel.
2. Rất nhiều thứ từ đất nứt, cánh chuồn chuồn, vỏ cà chua đến tổ ong đều có hình lục giác

Phía trên là tổ ong với những hình lục giác.
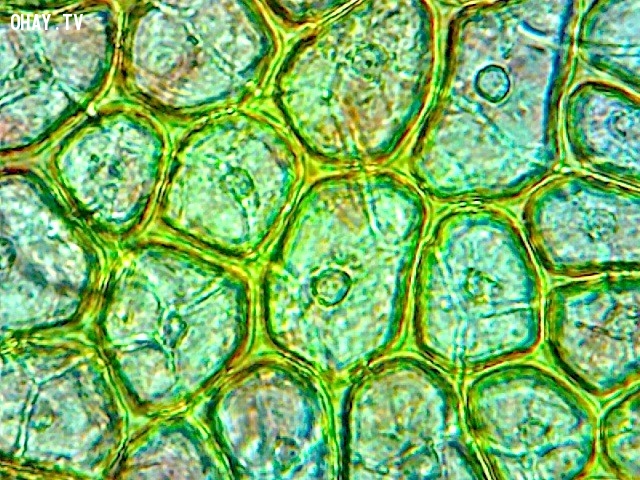
Còn đây là tế bào vỏ cà chua.

Còn đây là đất nứt.
Chuyện gì đã xảy ra? Các lập trình viên của Matrix đã lười biếng và tái sử dụng các cấu trúc tương tự?
Thực ra bạn sẽ không ngạc nhiên như vậy nếu bạn biết rằng bản chất của các cấu trúc hình lục giác đó là các Voronoi Diagram.
Trong toán học, một sơ đồ Voronoi là một cách phân tách một không gian metric theo khoảng cách tới một tập hợp rời rạc các vật thể cho trước trong không gian.
Trong trường hợp đơn giản nhất, khi các vật thể là các điểm, ta có một tập hợp S gồm các điểm trên mặt phẳng, được gọi là các điểm Voronoi. Mỗi điểm s ứng với một ô Voronoi, hay còn gọi là ô Dirichlet, kí hiệu là V(s), bao gồm tất cả các điểm gần s hơn tất cả các điểm Voronoi khác. Các cạnh của sơ đồ Voronoi là tập các điểm có khoảng cách tới hai điểm Voronoi gần nhất là như nhau. Các đỉnh của sơ đồ Voronoi là các điểm có khoảng cách tới ít nhất ba điểm Voronoi gần nhất là như nhau.
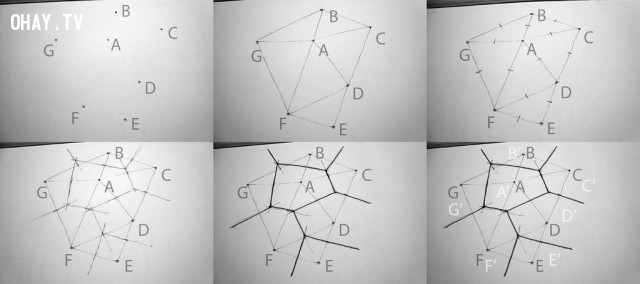
Nếu bạn vẫn còn khó hiểu, vậy thì hãy làm như sau (nhìn ảnh phía trên nếu có bước nào bạn không rõ):
- Bước 1: Dùng bút mực (hoặc bút bi) vẽ một số điểm ngẫu nhiên trên một mảnh giấy.
- Bước 2: Nối các điểm đó bằng các nét bút chì.
- Bước 3: Tại trung điểm của mỗi đoạn, bạn dùng bút mực (hoặc bút bi) vẽ các đoạn vuông góc sao cho chúng vừa đủ chạm vào nhau thì dừng.
- Bước 4: xóa hết các nét vẽ bằng bút chì. Thế là bạn đã có một sơ đồ Voronoi của riêng bạn.
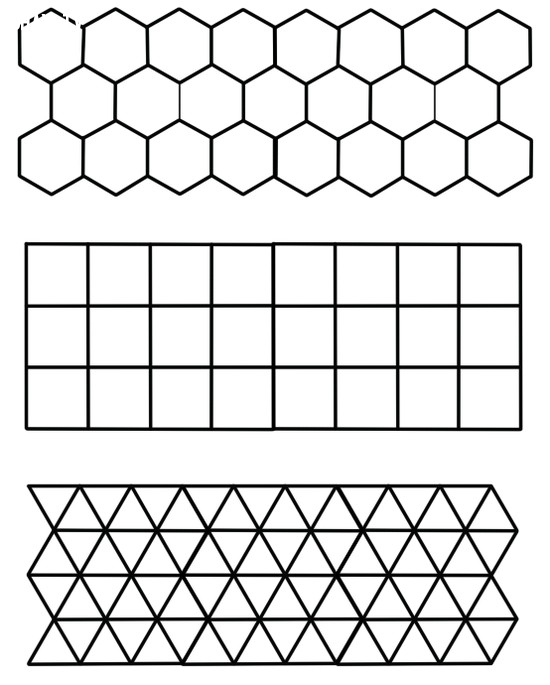
Chỉ có duy nhất 3 loại đa giác đều (kích thước không đổi) có thể dùng chính nó để điền vô hạn vào không gian hai chiều mà không bỏ trống bất cứ không gian nào, đó là: hình tam giác đều, hình vuông và hình lục giác đều (xem ảnh trên). Vùng không gian được lát bởi các đa giác đều có kích thước và hình dạng giống nhau đó được goi là tessellation.
Điều này dễ hiểu, bởi vì chỉ có 60 độ (góc của tam giác đều), 90 độ (góc của hình vuông) và 120 độ (góc của lục giác đều) là ước số của 360 độ. Trong khi đó góc của ngũ giác đều là 108 độ, góc của các đa giác nhiều hơn 6 cạnh thì lớn hơn 120 độ nhưng nhỏ hơn 180 độ. Do đó góc của ngũ giác đều và tất cả các đa giác đều khác không thể là ước số của 360 độ nên không thể tạo ra được tessellation.
Trong 3 loại cấu trúc đó thì cấu trúc lục giác là cấu trúc mạnh nhất và đòi hỏi vật liệu xây dựng ít nhất. Mỗi hình lục giác được bao bọc bởi 6 hình lục giác khác, và những hình lục giác bao bọc đến phiên chính nó lại được bao bọc bởi 6 hình lục giác.Cứ như vậy mở rộng ra vô hạn. Đó chính là cách thức con ong xây tổ và cũng là cách thức các loài thực vật xây dựng tế bào của chúng, nhưng không phải là cách chúng ta đóng gói hàng hóa. Bởi vì.... dường như những con ong và cây cối thông minh hơn chúng ta.
Và để cảm ơn cho sự theo dõi chăm chú nãy giờ của bạn, phía dưới là bộ lông mượt mà tuyệt đẹp của một con hươu cao cổ (với cấu trúc hình lục giác)

3. Động vật và thành phố tăng trưởng theo cùng một cách

Hãy tưởng tượng một con voi con. Và sau đó hãy tưởng tượng một thành phố đang có tốc độ phát triển nhanh chóng, ví dụ, hừm...TP.HCM. Hai đối tượng trên có điểm gì chung (ngoài thực tế rằng cả 2 sẽ sản xuất ra rất nhiều chất thải)? Điểm chung ở đây là: chúng phát triển theo cùng một cách chính xác như nhau.
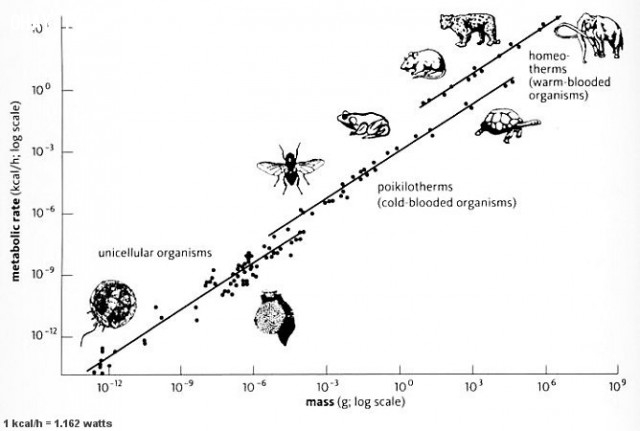
Theo như biểu đồ phía trên, chúng ta thấy được mối tương quan giữa mức độ trao đổi chất với độ dễ thương... à nhầm, tương quan giữa mức độ trao đổi chất với khối lượng cơ thể.
Mối tương quan đó tuân theo Luật Kleiber.
Luật Kleiber phát biểu rằng: mức độ trao đổi chất R của sinh vật tỷ lệ với khối lượng cơ thể M lũy thừa 3 phần 4.
R ~ M^3/4
Ví dụ một con mèo có khối lượng gấp 100 lần một con chuột nhắt, như vậy sự trao đổi chất của con mèo sẽ lớn hơn con chuột nhắt khoảng 32 lần.
Việc chứng minh Luật Kleiber liên quan đến nhiều phép tính toán học và sự tranh luận của các nhà khoa học về các phương pháp chứng minh khác nhau, chúng ta không nên tìm hiểu sâu quá làm gì.
Luật Kleiber được áp dụng cho hầu hết các sinh vật sống từ sinh vật đơn bào, thực vật, cá voi xanh và thậm chí là mẹ của bạn. Khi động vật phát triển lớn hơn, chúng trở nên tốt hơn trong việc lưu trữ và sử dụng năng lượng từ thực phẩm.
Trong một nỗ lực để dụ dỗ các nhà xã hội học chuyển sang nghiên cứu vật lý, nhà vật lý Geoffrey West cùng với băng đảng các cộng sự của ông đã khám phá ra một điều thú vị: nguyên tắc áp dụng cho sinh vật cũng áp dụng một cách y hệt cho các thành phố.
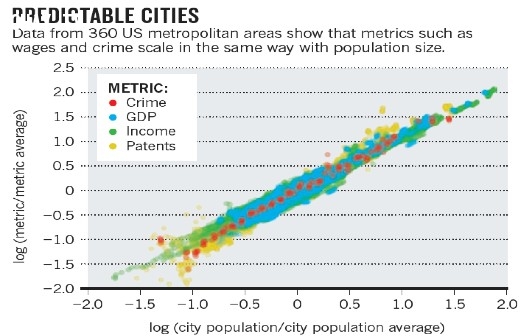
Tương tự như động vật, khi các thành phố phát triển lớn hơn, chúng cũng trở nên hiệu quả hơn trong việc xử lý năng lượng cần thiết. Hãy nghĩ về một ngôi làng nhỏ như một sinh vật đơn giản, ví dụ như một con bọ. So với các đối tác lớn của nó, nó cần rất ít nguồn lực để phát triển, tuy nhiên nó lại không thể quản lý nguồn lực đó một cách hiệu quả. Trong ngôi làng, mọi người sống trong những ngôi nhà nằm rải rác, hệ thống đường dây điện và ống dẫn nước là quá tốn kém so với quy mô của ngôi làng. Nhưng khi ngôi làng mở rộng và phát triển, nó càng ngày càng giống như một con vật lớn, ví dụ con voi. Một thành phố lớn là siêu hiệu quả trong việc quản lý con người, các tế bào của nó không còn là những túp lều rải rác mà là những tòa nhà chung cư, đại lộ là những mạch máu của nó, các con hẻm là mao mạch của nó, và các quan chức thành phố là... à mà thôi!
Sau ý tưởng đó, các nhà khoa học còn nghiên cứu ra các luật của sự nhân rộng đô thị, nó có thể dự đoán tính bền vững, tình trạng của một thành phố... và biết đâu trong tương lai, nó còn có thể dự đoán những thứ nhỏ nhặt hơn như dây cáp điện hoặc thu nhập cư dân thành phố.
Biết đâu lúc này, ở một nơi nào đó, một nhóm các nhà khoa học đang nghiên cứu một lý thuyết để dự đoán số tiền trong túi của bạn dựa trên sinh học của một con voi. Hãy cẩn thận!
4. Thương mại và trọng lực tuân theo những quy tắc tương tự nhau

Tiền bạc, kinh tế và thương mại luôn là những chủ đề nóng bỏng. Có rất nhiều cuốn sách về thương mại và những gì diễn ra bên trong nó được viết bởi những người đàn ông trong những bộ quần áo được thiết kế riêng và nở nụ cười bí hiểm. Nhưng bạn không cần phải quan tâm đến bất kỳ ai trong đám đó. Một đồng nghiệp của tôi tên là Isaac Newton đã viết hướng dẫn về chủ đề này từ tận thế kỷ 17 cơ. Được rồi, anh ta có thể gọi nó là "Lực hấp dẫn", nhưng đừng để bị đánh lừa. Anh chàng này là một tay tài phiệt chính hãng cải trang thành một thiên tài.
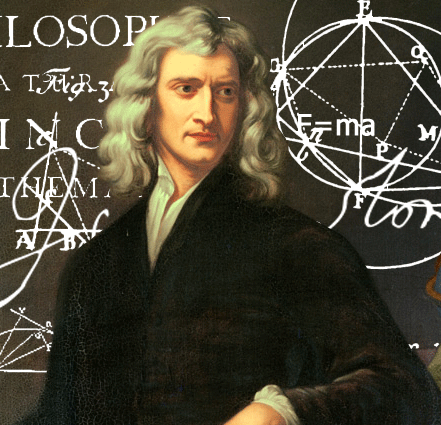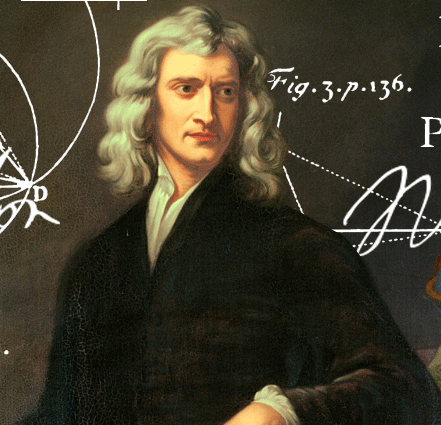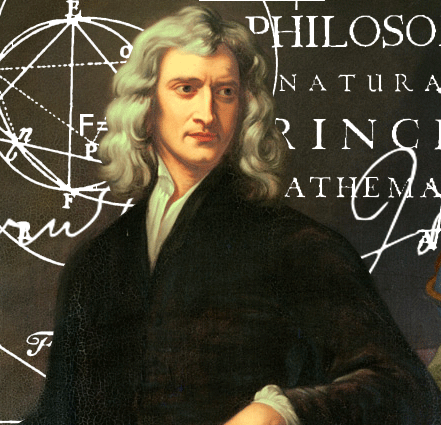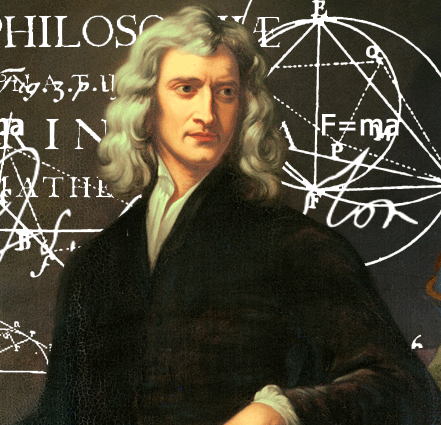
Mô hình của lực hấp dẫn rất đơn giản: lực hấp dẫn giữa 2 đối tượng tỷ lệ thuận với khối lượng của chúng và tỷ lệ nghịch với khoảng cách giữa chúng.
Quy tắc trên cũng áp dụng đối với thương mại, chỉ với một thay đổi nhỏ, thay "khối lượng" bằng "GDP". Hai nước có quan hệ thương mại càng lớn nếu GDP của họ càng lớn và khoảng cách giữa họ càng gần.
Điều này rõ ràng khi bạn thực hiện kết nối. Vận chuyển hàng hóa thì đắt như quỷ, vì vậy các công ty cảm thấy dễ dàng hơn để có quan hệ thương mại với những nước gần họ nhất. Thỉnh thoảng, một vài công ty hoặc cá nhân sẽ tạo thành ngoại lệ, nhưng mô hình trọng lực chung vẫn đúng cho toàn bộ đất nước.
Canada cho đến nay là đối tác thương mại lớn nhất của Mỹ, với giá trị thương mại 632 tỷ USD năm 2013, trong khi đó giá trị thương mại giữa Mỹ và Nhật Bản chỉ có 204 tỷ USD mặc dù GDP của Nhật Bản gấp 3 lần Canada. Tất nhiên còn có những yếu tố khác đóng vai trò ở đây ngoài GDP và khoảng cách, ví dụ như quan hệ giữa các nước, giá cả, ngôn ngữ, khả năng nước này đánh bom nước kia... nhưng về cơ bản, yếu tố GDP và khoảng cách là 2 yếu tố quan trọng nhất.
Nếu bạn muốn nghiên cứu sâu hơn về khía cạnh toán học của mô hình trọng lực trong thương mại, hãy vào Google gõ từ khóa "Gravity model of trade".
5. Bạn có thể sử dụng các cơn dư chấn động đất để dự đoán tội phạm

Con người vốn khó đoán. Nhưng có một cách đơn giản để dự đoán hành vi của những kẻ khó đoán nhất trong tất cả mọi người: những tên tội phạm. Có thể đọc tới đây bạn sẽ nghĩ: "Nhảm nhí! Nếu có một cách như thế, cảnh sát đã bắt hết hàng buôn lậu của tôi rồi!". Vâng, tốt nhất là bạn hãy cố gắng thực hiện thêm vài phi vụ buôn lậu lớn nữa, bởi vì sự nghiệp tội phạm của bạn sắp đi đến hồi kết rồi! Và đó là gì? Một thuận toán dùng để dự đoán sự chuyển động của các loại đá.
Khi một trận động đất xảy ra ở một khu vực, khu vực đó sẽ có khả năng xảy ra dư chấn trong một khoảng thời gian sau đó. Dự đoán động đất thì khó khăn, nhưng dự đoán những cơn dư chấn thì dễ dàng hơn nhiều. Trong thực tế, có một mô hình toán học đáng tin cậy để làm việc đó. Dưới đây là một điều thú vị mà Sở cảnh sát Los Angeles và Santa Cruz đã phát hiện trong năm 2014: Các mô hình y hệt cũng có thể áp dụng để dự đoán tội phạm.
Hãy tưởng tượng rằng có một tên tội phạm đột nhập vào nhà bạn và ăn cắp toàn bộ đám chó cảnh quý hiếm của bạn. Hãy đóng kín cửa sổ, gia cố lại tường rào hoặc làm bất cứ điều gì để bảo vệ tài sản của bạn, bởi vì bạn sẽ ngạc nhiên về số lượng những vụ phạm tội khác sẽ sớm xảy ra trong khu phố của bạn. Kẻ trộm bây giờ đã biết khu vực này là một mục tiêu hấp dẫn, đã biết rõ vị trí các ngôi nhà cũng như các lối thoát hiểm tiềm năng. Hắn thậm chí còn có thể trở lại để lấy cắp đám vẹt đuôi dài của bạn, bởi vì hắn đã quen thuộc với các bố trí nhà và thói quen của bạn. Những điểm nóng của các vụ phạm tội lặp lại tuân theo mô hình tương tự như các cơn dư chấn động đất.
Sở cảnh sát Los Angeles và Santa Cruz đã sử dụng phân tích Big Data cho 13 triệu báo cáo tội phạm từ 80 năm qua, và kết quả là nó tạo ra một mô hình giống hệt như mô hình toán học dự báo địa chấn. Sử dụng dữ liệu này vào các vụ tuần tra ưu tiên, họ đã giảm các vụ trộm cắp xuống 33%, các vụ phạm tội bạo lực 21% và các vụ phạm tội liên quan đến tài sản 12%. Không ngạc nhiên, rất nhiều thành phố khác ở Mỹ sau đó cũng bắt đầu sử dụng mô hình này để dự đoán tội phạm.
Ngay bây giờ, hệ thống vẫn chỉ có thể được sử dụng để dự đoán mô hình của những người đã phạm tội, những người đã có tiếp xúc với hệ thống tư pháp. Vì vậy, không cần phải lo lắng, miễn là họ chưa bao giờ bắt được bạn, họ sẽ không thể áp dụng hệ thống này để dự đoán được hành vi phạm tội của bạn.
------------------------------------------------------------------------------------
Cảm ơn tất cả những độc giả đã kiên trì đọc tới cuối bài.
Bài viết này được viết theo phong cách hài hước và đôi khi chêm vào vài câu bông đùa nhảm nhí, tuy nhiên tất cả các kiến thức khoa học trong bài viết đều có độ chính xác rất cao. Tôi đã mất hơn 4 tiếng đồng hồ để hoàn thành bài viết này, chưa kể thời gian nghiên cứu tư liệu tham khảo. Nếu thấy hay, tiếc gì mà không nhấn nút Share lên Facebook nhỉ?
Biên soạn: Woody Übermensch - Ohay TV
*****************************
Các bài viết khác có thể bạn sẽ thích:
