5 nghịch lý 'hại não nhất', liệu bạn có lý thể lý giải được?

1. Nghịch lý ông nội

Nghịch lý ông nội lần đầu tiên được miêu tả bởi nhà khoa học giả tưởng René Barjavel trong quyển sách Le Voyageur Imprudent  (nhà du hành khinh suất) xuất bản năm 1943. Nội dung của nghịch lý này là: “Có một người đàn ông du hành thời gian về quá khứ và giết ông nội mình trước khi ông mình cưới bà nội. Kết quả là cha của anh ta sẽ không được sinh ra, điều đó dẫn tới người đàn ông đó sẽ không bao giờ được ra đời thì sao anh có thể du hành về quá khứ. Nhưng nếu anh không về quá khứ để giết ông nội mình thì ông nội anh phải còn sống và điều đó nghĩa là anh vẫn được ra đời và có thể vượt thời gian để giết ông nội mình”. Hai tình trạng trên đã phủ nhận sự tồn tại của cả hai trường hợp, đây là một loại của logic nghịch lý.

Lý thuyết nghịch lý ông nội là một minh chứng bác bỏ khả năng du hành thời gian về quá khứ. Tuy nhiên, đã có một số phương pháp dùng để giải mã câu đố này đã được công bố, như là lý thuyết thời gian bất khả đổi nghĩa là tất cả mọi thứ trong thế gian đều đã sắp đặt không ai có thể thay đổi gì hết hoặc là khái niệm vũ trụ là một khoảng thời gian và không gian song song.

Một nghịch lý có liên quan là Nghịch lý Hitler hoặc Nghịch lý vụ ám sát Hitler. Nghịch lý Hitler này được thấy trong các thể loại khoa học giả tưởng, khi một người hùng vai chính du hành về quá khứ để giết chết Hitler trước khi Hitler tạo nên chiến tranh thế giới hai. Nếu như chiến tranh thế giới thứ hai chưa từng xảy ra thì lý do quay về quá khứ để giết Hitler cũng sẽ không hề tồn tại.

2. Nghịch lý Zeno - Achilles và con rùa

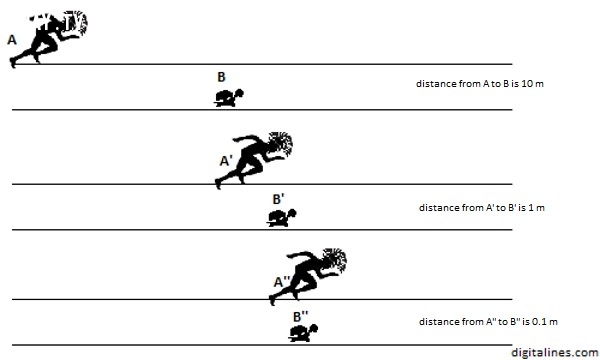
Trong nghịch lý Achilles và rùa, Achilles chạy đua với rùa. Ví dụ Achilles chấp rùa một đoạn 100 mét. Nếu chúng ta giả sử rằng mỗi tay đua đều bắt đầu chạy với một tốc độ không đổi (Achilles chạy rất nhanh và rùa rất chậm), thì sau một thời gian hữu hạn, Achilles sẽ chạy được 100 mét, tức anh ta đã đến được điểm xuất phát của con rùa. Nhưng trong thời gian này, con rùa cũng đã chạy được một quãng đường ngắn, ví dụ 10 mét. Sau đó Achilles lại tốn một khoảng thời gian nữa để chạy đến điểm cách 10 mét ấy, mà trong thời gian đó thì con rùa lại tiến xa hơn một chút nữa, và cứ như thế mãi. Vì vậy, bất cứ khi nào Achilles đến một vị trí mà con rùa đã đến, thì con rùa lại cách đó một đoạn. Bởi vì số lượng các điểm Achilles phải đến được mà con rùa đã đi qua là vô hạn, do đó anh ta không bao giờ có thể bắt kịp được con rùa. Trên thực tế, điều này thật vô lý vì nếu bạn chạy đua với 1 con rùa thì bạn rõ ràng có thể vượt nó một cách dễ dàng nhưng nếu suy luận theo cách “hại não” của nghịch lý này thì rõ ràng, bạn không bao giờ có thể vượt nó.

“Trong một cuộc chạy đua, người chạy nhanh nhất không bao giờ có thể bắt kịp được kẻ chậm nhất. Kể từ khi xuất phát, người đuổi theo trước hết phải đến được điểm mà kẻ bị đuổi bắt đầu chạy. Do đó, kẻ chạy chậm hơn luôn dẫn đầu.”  – theo lời ghi lại của Aristotle

3. Nghịch lý Ngày hành quyết bất ngờ

Nghịch lý Ngày hành quyết bất ngờ là một trong những nghịch lý logic đã làm vô số các nhà bác học từ cổ chí kim đau đầu vì sự khó hiểu của nghịch lý này. Nội dung nghịch lý như sau: Tại một phiên tòa, thẩm phán ra phán quyết đối với người tử tù rằng anh ta sẽ bị treo cổ vào giữa trưa một ngày thường (từ thứ Hai đến thứ Sáu) trong tuần sau. Ngày hành quyết sẽ là một bất ngờ đối với người tử tù và anh ta chỉ có thể biết được khi cai ngục đến gõ cửa buồng ngay trước giờ ra pháp trường.

Sau khi ngẫm nghĩ về bản án, người tù tự kết luận rằng anh ta sẽ thoát chết. Lý luận của anh ta đưa ra như sau: Theo như bản án, ngày hành quyết sẽ hoàn toàn “bất ngờ” đối với anh ta. Như vậy anh ta sẽ không thể bị treo cổ vào ngày thứ 6 (ngày cuối cùng có thể hành quyết trong thời hạn 5 ngày) vì như vậy không bất ngờ chút nào. Tương tự, anh không thể bị treo cổ vào ngày thứ 5 (ngày cuối cùng trong thời hạn hành quyết 4 ngày – vì ngày thứ 6 không treo cổ được rồi nên 5-1 =4).  Cứ như vậy anh tiếp tục cách suy luận này và áp dụng cho các ngày còn lại trong tuần, và kết luận rằng mình chắc chắn sẽ không thể bị hành quyết. Anh ta liền vui vẻ quay trở về buồng ngục của mình hoàn toàn yên tâm đánh một giấc ngon lành. Vài ngày sau, cai ngục đến gõ cửa buồng anh ta vào trưa ngày thứ Tư,  và anh ta bị lôi ra pháp trường. Như vậy, suy luận của người tử tù này sai ở đâu ?

4. Nghịch lý Người nói dối

Được tạo ra bởi người thợ mộc già Mister Geppetto trong một ngôi làng nhỏ của Ý, chú rối gỗ Pinocchio mơ ước trở thành một cậu bé bằng xương bằng thịt. Cậu thường hay nói dối và bịa đặt ra những câu chuyện vì nhiều lý do khác nhau, mỗi khi cậu bé nói dối, mũi cậu sẽ dài ra. Vậy trong trường hợp này, khi cậu nói “Mũi của cháu sẽ dài ra ngay bây giờ”, nếu mũi dài ra nghĩa là cậu bé đã nói thật như vậy mũi sẽ không dài ra. Nếu mũi không dài ra, nghĩa là Pinocchio nói dối, như vậy mũi lại dài ra. Và như thế vòng luẩn quẩn cứ lập đi lập lại.

5. Nghịch lý Mũi tên bay

Về cơ bản Zeno cho rằng mọi vật không chuyển động . Trong nghịch lý mũi tên, Zeno nói rõ rằng để chuyển động xảy ra, thì đối tượng phải thay đổi vị trí mà nó chiếm giữ. Ông đã đưa ra ví dụ về một mũi tên đang bay. Ông lập luận rằng trong bất kỳ một khoảnh khắc (thời điểm) nào đó thì mũi tên không di chuyển đến vùng không gian nó đang chiếm, và cũng không di chuyển đến vùng không gian mà nó không chiếm. Nó không thể đang di chuyển đến nơi mà nó không chiếm, bởi vì thời gian không trôi để nó di chuyển đến đó, nó cũng không thể đang di chuyển đến nơi nó đang chiếm, bởi vì nó đã đứng đó rồi. Nói một cách khác thì tại mỗi khoảnh khắc của thời gian, không có chuyển động xảy ra. Nếu mọi vật đều bất động trong mỗi khoảnh khắc, và thời gian hoàn toàn là bao gồm các khoảnh khắc, thì chuyển động là không thể xảy ra.

"Nếu tất cả mọi thứ đều chiếm một khoảng không gian khi nó đứng yên, và nếu khi nó chuyển động thì nó cũng chiếm một khoảng không gian như thế tại bất cứ thời điểm nào, do đó mũi tên đang bay là bất động". - theo lời ghi lại của Aristotle

Xem thêm bài viết thú vị khác tại đây

• 99% trả lời sai bức ảnh cuối, còn bạn thì sao?
  
• Những lời phê BÁ ĐẠO nhất của thầy cô
  
• Những hình ảnh đáng sợ được phát hiện trên Google Maps
  
• Sao Việt và những phát ngôn gây sốc về TIỀN